红黑树
红黑树是一种自平衡的二叉查找树(BST),可在O(logN)时间内完成查找、插入、删除等操作。
鉴于插入操作比较容易理解,删除操作相对较难,这里只描述删除节点的操作。
红黑树性质
红黑树通过如下规则,控制任意节点的左右子树高度差,以实现自平衡:
- 节点是红色或黑色。
- 根节点为黑色。
- 如果节点为红,其子节点必须为黑(每个叶节点到根节点所有路径上不能有两个连续的红色节点)。
- 任一节点至树尾端的所有简单路径,所含黑节点数必须相同。
删除节点
旋转
旋转操作在红黑树的插入和删除中都会使用
- 左旋:将节点旋转为其右孩子的左孩子
- 右旋:将节点旋转为其左孩子的右孩子
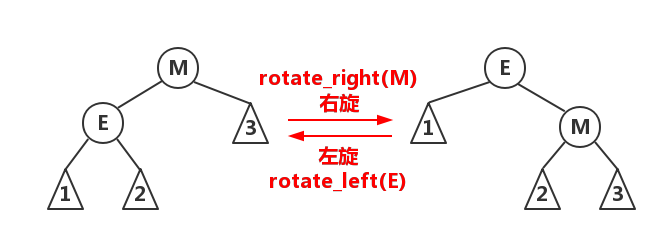
删除
删除操作首先要确定待删除节点的孩子数。
case 1:待删除节点有两个孩子。
找到该节点的前驱或后继,将前驱或后继的复制到待删除节点中,最后将这个前驱或后继删除。由于前驱或后继至多只有一个孩子节点,问题就被简化为case 2。只要节点里的值被删除就行,树结构发生变化并不影响。case 2:待删除节点只有一个孩子或没有孩子。
直接让它的孩子取代待删节点的位置即可。
红黑树删除操作的复杂度在于删除节点的颜色。case 2.1:删除的节点是红色。
直接拿其孩子节点补空位即可。case 2.2:删除的节点是黑色。
所有经过该节点的路径上的黑色节点数量少了一个,破坏了性质4。此时需要重新平衡红黑树,具体见下。
删除后重平衡
说明之前,首先假设最终被删除的节点为Z(至多一个孩子节点),其孩子节点为X。删除黑色节点Z,X取代Z后,假设X的父节点(原来Z的父节点)为P,X的兄弟节点为W,W的左孩子为WL,右孩子为WR。
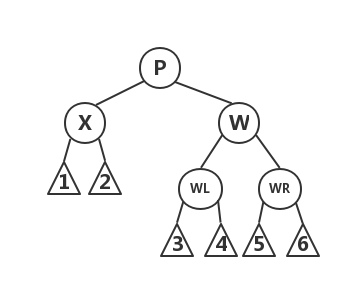
假设X为P的左孩子,X是右孩子的情况只需与之对称操作即可,下面对各种情况展开讨论:
case 1:X是红色或为新的根节点。(终止情况)
直接将其变为黑色即可,这样分别恢复了性质4和性质2。
剩下都是X为黑色的情况,需要考虑X的兄弟W的颜色。case 2:W为红色,X为黑色。
由性质3可知,节点P、WL、WR必为黑色。
对P左旋,互换P和W的颜色,节点W重新指向X当前的兄弟WL。此时所有路径的黑色节点数并未受到影响,即经过X的路径(路径1、2)上的黑色节点依然比其他路径少一个,和删除Z之后一样。但已经将该情况转变为case 3,再根据当前黑色W的两个孩子的颜色继续调整。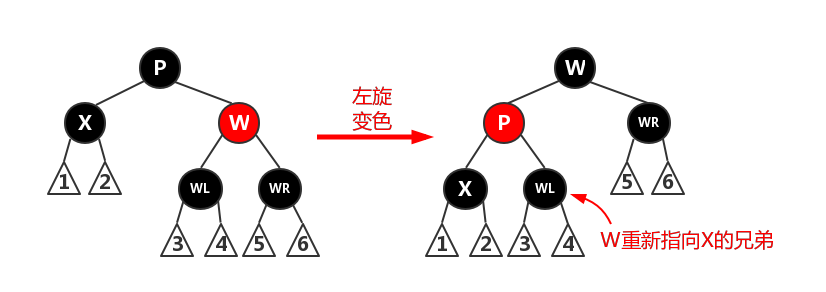
case 3:W为黑色,X为黑色。case 3.1:W的孩子节点WL、WR均为黑色。case 3.1.1:P为黑色。
只需把W变为红色,这样所有经过W的路径(路径3~6)比之前少一个黑色节点,就与经过X的路径(路径1、2)上的黑色节点数一致了。但经过P的路径(1~6)比不经过P的路径少一个黑色节点,再把X节点指向P,从case 2开始重新进行平衡处理。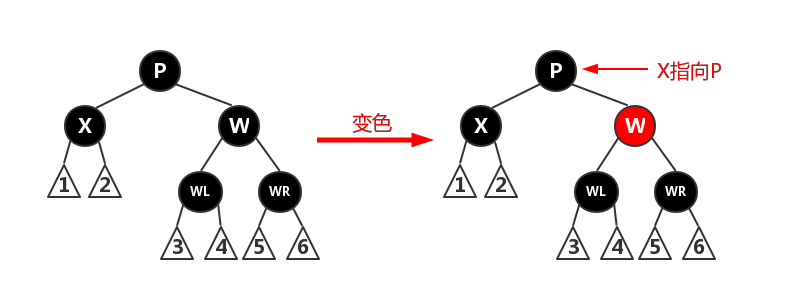
case 3.1.2:P为红色。(终止情况)
只需互换W和P的颜色即可。因为P变为黑色,经过X的路径(路径1、2)多了一个黑色节点,与删除Z节点前的数量一致。而其他路径(路径3~6)上的黑色节点数并未受到影响,因此红黑树恢复性质4,重平衡完毕。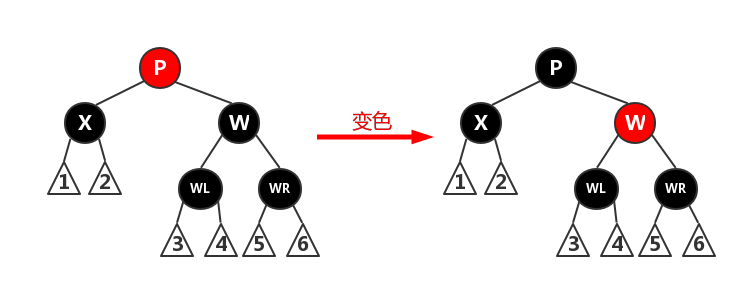
case 3.2:W的孩子节点有红色,P可红可黑。case 3.2.1:WL为红色,WR为黑色。
对W进行右旋操作,并互换W和WL的颜色,此时所有路径的黑色节点数并未受到影响,但将该情况转化为case 3.2.2。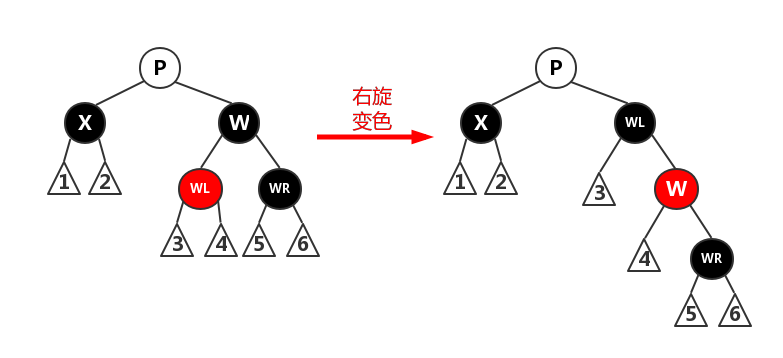
case 3.2.2:WR为红色,WL可红可黑。(终止情况)
对P进行左旋操作,并互换P和W的颜色,并将WR变为黑色。因为P变为黑色,经过X的路径(路径1、2)多了一个黑色节点,与删除Z节点前的数量一致。而其他路径(路径3~6)上的黑色节点数并未受到影响,因此红黑树恢复性质4,重平衡完毕。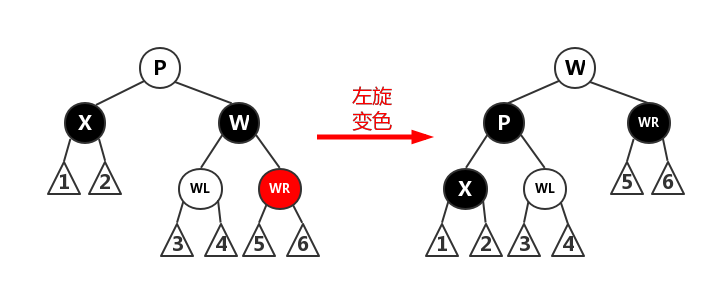
总结
学习红黑树时,发现许多数据结构相关书籍,包括《STL源码剖析》都没有详细分析红黑树的删除操作。网上博客的许多资料总觉得不够清晰,关于删除节点后重新平衡这一关键步骤讲得不够有条理。总之,case 1、case 2、case 3通过相互转化,不断调整红黑树,最终转化成终止情况case 1、case 3.1.2、case 3.2.2结束调整。具体代码可以参见我 github 中实现的 TinySTL 中的tree.h头文件。