凸包
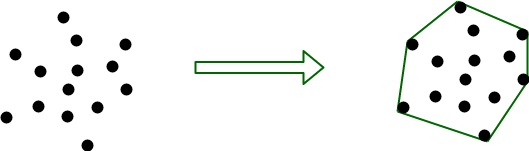
凸包(Convex Hull)是一个计算几何(图形学)中的概念。点集Q的凸包是指一个最小凸多边形,满足Q中的点或者在多边形边上或者在其内。
正式讨论凸包问题之前,这里先引入一个辅助概念——“方向”。
有序点的方向
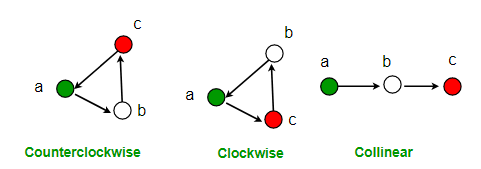
一个平面内有序点的方向(Orientation)可以有三种:
- 逆时针 CounterClockwise
- 顺时针 Clockwise
- 共线 Colinear
对于点$a(x_1, y_1)$、$b(x_2, y_2)$、$c(x_3, y_3)$,线段$ab$的斜率为
$$ \sigma = \frac{y_2 - y_1}{x_2 - x_1} $$
线段$bc$的斜率为
$$ \tau = \frac{y_3 - y_2}{x_3 - x_2} $$
- 若$ \sigma < \tau $,方向是逆时针(向左转)
- 若$ \sigma = \tau $,方向是共线
- 若$ \sigma > \tau $,方向是顺时针(向右转)
因此,三个有序点的方向依赖于表达式
$$ (y_2 - y_1) \times (x_3 - x_2) - (y_3 - y_2) \times (x_2 - x_1) $$
- 若表达式为负,方向是逆时针
- 若表达式为0,方向是共线
- 若表达式为正,方向是顺时针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
struct Point
{
int x;
int y;
};
/* -1 逆时针
0 共线
1 顺时针 */
int Orientation(const Point& p, const Point& q, const Point& r)
{
int v = (q.y - p.y) * (r.x - q.x) - (r.y - q.y) * (q.x - p.x);
return v ? v / abs(v) : v;
}
|
两线段相交
利用上述方向的概念,很容易判断两线段 (p1, q1) 和 (p2, q2) 是否相交。
(p1, q1, p2) 和 (p1, q1, q2) 方向不同并且 (p2, q2, p1) 和 (p2, q2, q1) 方向不同。
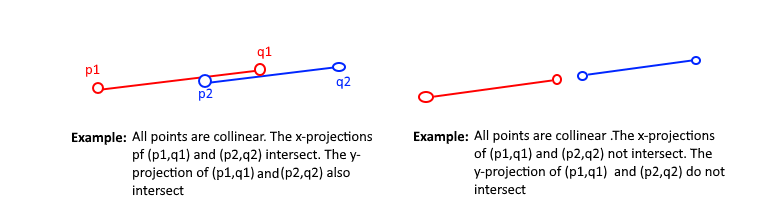
(p1, q1, p2)、(p1, q1, q2)、(p2, q2, p1) 和 (p2, q2, q1) 4 个方向均共线并且
- (p1, q1) 和 (p2, q2) 的 x 轴部分相交
- (p1, q1) 和 (p2, q2) 的 y 轴部分相交
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
// 给定p、q、r三点共线,判断q是否在线段pr上
bool OnSegment(const Point& p, const Point& q, const Point& r)
{
if (q.x <= max(p.x, r.x) && q.x >= min(p.x, r.x) &&
q.y <= max(p.y, r.y) && q.y >= min(p.y, r.y))
return true;
return false;
}
// 判断线段ab与线段cd是否相交
bool Intersect(const Point& a, const Point& b, const Point& c, const Point& d)
{
int o1 = Orientation(a, b, c);
int o2 = Orientation(a, b, d);
int o3 = Orientation(c, d, a);
int o4 = Orientation(c, d, b);
if (o1 != o2 && o3 != o4)
return true;
// a、b、c共线且c在线段ab上
if (o1 == 0 && OnSegment(a, c, b)) return true;
if (o2 == 0 && OnSegment(a, d, b)) return true;
if (o3 == 0 && OnSegment(c, a, d)) return true;
if (o4 == 0 && OnSegment(c, b, d)) return true;
return false;
}
|
2D凸包问题
凸包问题最常见的两种解法是 Jarvis 步进法和 Graham 扫描法,有了上面的基础,这两种方法很容易实现出来。
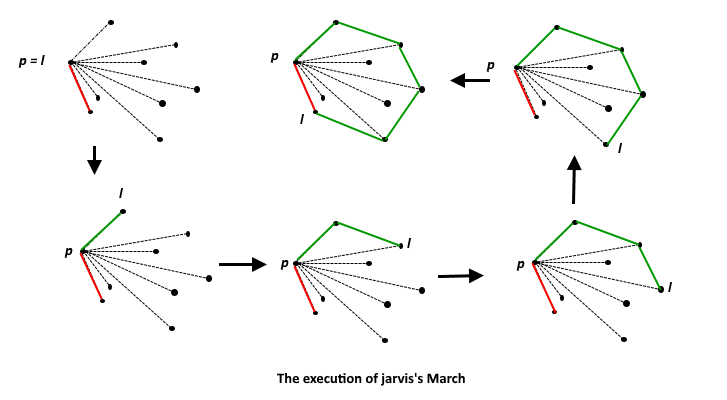
Jarvis’s Algorithm or Wrapping
算法流程如下:
- 初始化 p 为最左侧的点(x 坐标最小的点)
- 循环如下步骤,直到回到初始的最左侧的点
- 找到下一个点 q,使得对于任意其他点 r,有三元组 (p, q, r) 的方向是逆时针,这里就要用到上面方向的概念
- 存储 q 作为 p 的下一个输出元素
- p = q
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
void ConvexHull1(const vector<Point>& points, vector<Point>& hull)
{
size_t n = points.size();
if (n < 3) return;
size_t leftmost = 0;
for (size_t i = 1; i < n; ++i)
if (points[i].x < points[leftmost].x)
leftmost = i;
size_t p = leftmost;
do {
hull.push_back(points[p]);
size_t q = (p + 1) % n;
// 找到q,相对于p是最逆时针的
for (size_t i = 0; i < n; ++i) {
// p->i->q方向为逆时针,因此i比q更加逆时针,更新q
if (Orientation(points[p], points[i], points[q]) < 0)
q = i;
}
p = q;
} while (p != leftmost);
}
|
算法的复杂度为 O(m * n),其中 m 是输出凸包中点的数量,n 是输入点集中点的数量。最坏的情况下,点集中所有点都在输出的凸包上,时间复杂度为 O(n^2)。
Graham Scan
算法可以分为两个主要部分:
预处理
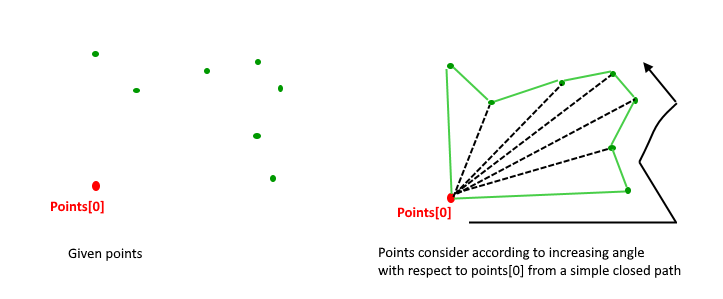
- 找到最下方的点(y 坐标最小的点),若有 y 坐标相同,则取 x 坐标较小的点。使该点 p0 作为输出凸包的第一个元素 points[0]。
- 将剩下 n - 1 个点排序,以 p0 到该点与 x 轴的逆时针夹角从小到大的顺序排序,若有角度相同,则将距离 p0 较近的点放在前面。
- 看是否有多个点有相同角度,移除它们,仅保留距离 p0 最远的那个点。此时得到的数组 points 是一条闭合路径。
接受或拒绝点
- 创建空栈 S,将 points[0]、points[1]、points[2] 入栈。
- 处理剩余的每个 points[i]:
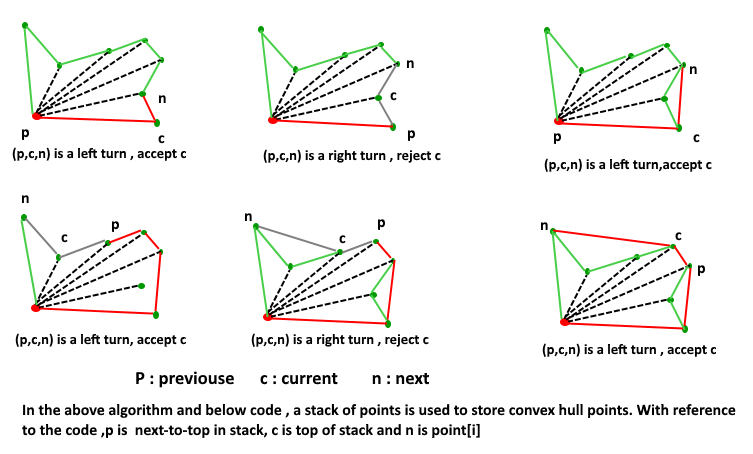
- 追踪当前的三个点 prev(p):栈顶的下一个点,curr©:位于栈顶的点,next(n):points[i],如果它们的方向不是逆时针(向左转),则移除当前栈顶的点 c,否则保留。
- 将 points[i] 入栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
|
// 交换两个点
void Swap(Point &lhs, Point &rhs)
{
Point temp = lhs;
lhs = rhs;
rhs = temp;
}
// 返回两个点的距离的平方
int DistSq(const Point& lhs, const Point& rhs)
{
return (lhs.x - rhs.x) * (lhs.x - rhs.x) + (lhs.y - rhs.y) * (lhs.y - rhs.y);
}
// 用于Compare的全局变量
Point p0;
// 排序比较函数,比较与全局变量p0的角度
// p0p1角度 < p0p2角度,返回-1
// p0p1角度 > p0p2角度,返回 1
int Compare(const void* lhs, const void* rhs)
{
Point* p1 = (Point*)lhs;
Point* p2 = (Point*)rhs;
int o = Orientation(p0, *p1, *p2);
if (o == 0)
return (DistSq(p0, *p1) <= DistSq(p0, *p2)) ? -1 : 1;
else
return (o < 0) ? -1 : 1;
}
// 返回栈顶的下一个Point
Point NextToTop(stack<Point> &S)
{
Point p = S.top();
S.pop();
Point res = S.top();
S.push(p);
return res;
}
void ConvexHull2(vector<Point> points, vector<Point>& hull)
{
size_t n = points.size();
// 找到最下方的点,优先左边
size_t bottommost = 0;
int ymin = points[0].y;
for (size_t i = 1; i < n; ++i)
{
int y = points[i].y;
if (y < ymin || (ymin == y && points[i].x < points[bottommost].x))
ymin = points[i].y, bottommost = i;
}
// 将其换到第一个位置
Swap(points[0], points[bottommost]);
// 用Compare排序
p0 = points[0];
qsort(&points[1], n - 1, sizeof(Point), Compare);
// 若有多个点与p0角度相同,仅留下距p0最远的那个
int num = 1; // 记录删除元素后points的元素数量
for (size_t i = 1; i < n; ++i) {
// 当i与i + 1角度相同,则一直移除i
while (i < n - 1 && Orientation(p0, points[i], points[i + 1]) == 0)
i++;
points[num] = points[i];
num++;
}
if (num < 3) return;
stack<Point> S;
S.push(points[0]);
S.push(points[1]);
S.push(points[2]);
for (int i = 3; i < num; i++) {
// 若栈顶第二个点、栈顶点、points[i]的方向不是逆时针
// 则一直移除栈顶点
while (Orientation(NextToTop(S), S.top(), points[i]) >= 0)
S.pop();
S.push(points[i]);
}
// 栈S中元素即为输出
hull.resize(S.size());
int i = 0;
while (!S.empty()) {
hull[i++] = S.top();
S.pop();
}
}
|
算法的第 1.1 步(找到最下方的点)花 O(n) 时间,第 1.2 步(点的排序)花 O(n * logn) 时间,第 1.3 步花 O(n) 时间。第 2 个步骤中,每个元素入栈和出栈最多一次,假设栈操作 O(1) 时间,则第 2 步总共花 O(n) 时间。因此总体的时间复杂度是 O(n * logn)。